Aston 1922/Chapter 5
Chapter V - The Mass-Spectrograph
Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.
30. Limitations of the parabola method
The parabola method of analysis of positive rays described in Chapter III, though almost ideal for a general survey of masses and velocities, has objections as a method of precision, many rays are lost by collision in the narrow canal-ray tube; the mean pressure in which must be at least half that in the discharge-bulb; very fine tubes silt up by disintegration under bombardment; the total energy available for photography falls off as the fourth power of the diameter of the canal-ray tube.
The first two objections can be overcome, as will be described below, by replacing the brass or copper tube by fine apertures made in aluminium, a metal which appears to suffer little disintegration, and by exhausting the space between these apertures to the highest degree by means of a subsidiary charcoal tube or pump. The falling off in intensity of the parabolas as one attempts to make them finer is a very serious difficulty, as the accuracy and resolving power depend on the ratio of the thickness to the total magnetic deflexion; and if we increase the latter the electric deflexion must be increased to correspond and the parabolas are drawn out, resulting again in loss of intensity.
Also the nature of the patch thrown on the plate by the use of a long circular tube will clearly be the same as that caused by the fight from an evenly illuminated disc passing through a circular aperture of the same diameter, that is to say it will have a penumbra. Similarly the parabolic streak produced by an infinite series of such patches will not be particularly suitable for accurate measurements as it has no definite edges.
31. Methods of increasing the intensity of the spot
The concentration of the stream of positive rays down the axis of the discharge-bulb is very marked, but there is good evidence for assuming that the intense part of the stream occupies a considerable solid angle. This suggests the possibility of an increase of intensity by means of a device which should select the rays aimed at a particular spot on the plate, whatever direction they come from. For example, a thin gap between two coaxial equiangular cones would allow the rays to be concentrated at the vertex. The dimensions of the patch formed would be roughly those of one given by a cylindrical canal-ray tube of diameter equal to the width of the gap. The increase of intensity would therefore be considerable; but the method is not easy to put into practice, and, in the case of deflexions through large angles, would necessitate a curved photographic surface.
Clearly the simplest way of increasing the intensity of the spot without increasing its dimensions, at any rate in one direction, is to use two parallel straight slits. In the case of the parabola method this device would only be of use in a special case such as the resolution of a close double, as the parabolas will only be sharp at points where they are parallel to the slit.
Such a slit system eliminates the difficulty of the penumbra mentioned above, at any rate so far as measurements at right angles to the line image are concerned.
32. Possibilities of "focussing."
Beams of charged particles which are homogeneous electrically (constant ) or magnetically (constant ) can be focussed like rays of light by special devices.[1] The method of Dempster, described in the previous Chapter, makes use of a form of magnetic focussing. But the rays generated by the ordinary discharge bulb are heterogeneous both in and so that what is required is an arrangement which will focus all rays of constant mass, even though their velocity may vary over an appreciable range.
33. Principle of the Mass-spectrograph
This purpose is achieved by the arrangement illustrated diagrammatically in Fig. 8. The exact mathematical analysis has now been worked out by R. H. Fowler,[2] but it is proposed to give only the approximate theory here for the sake of simplicity.
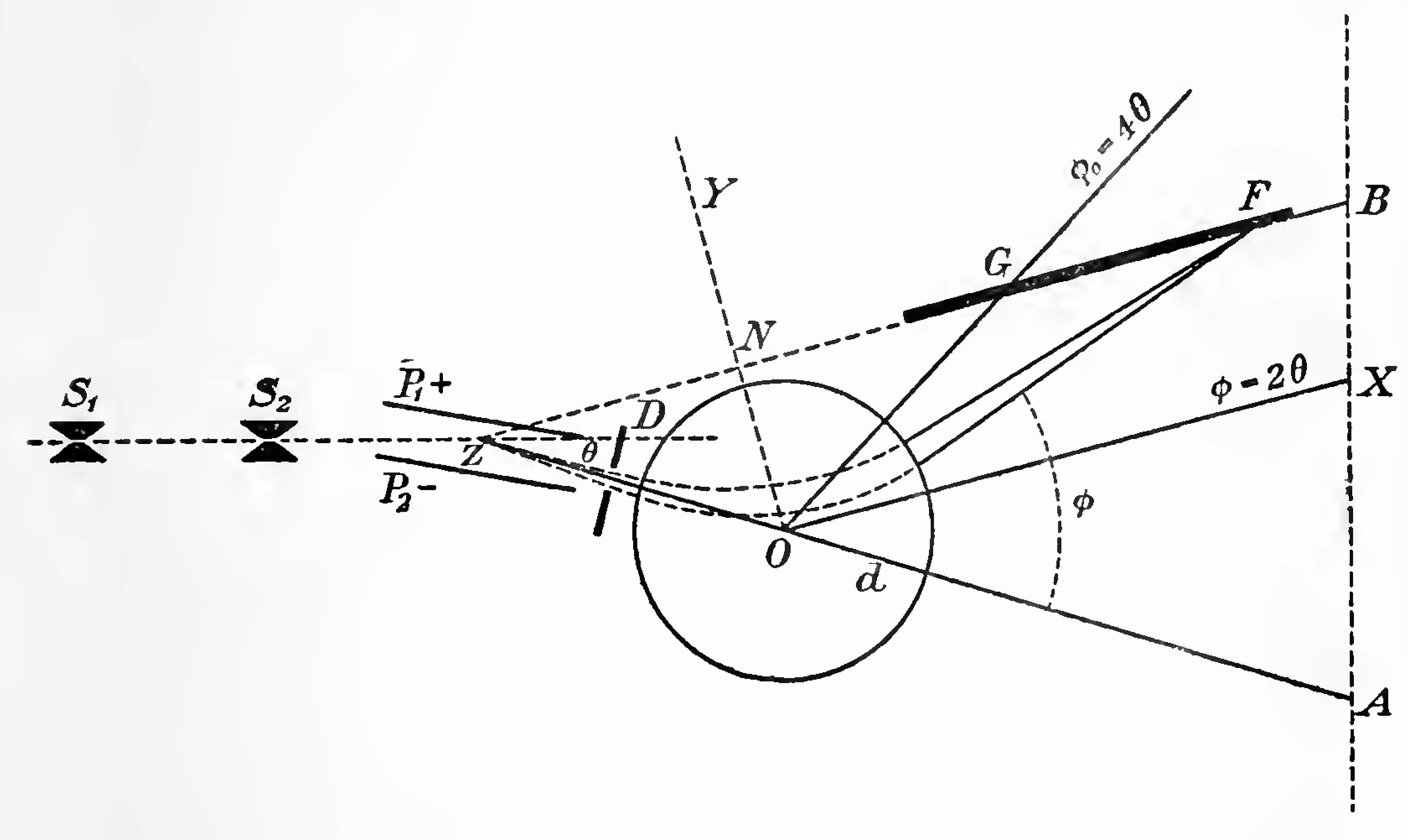
The rays after arriving at the cathode face pass through two very narrow parallel sUts of special construction Si S3, and the resulting thin ribbon is spread out into an electric spectrum by means of the parallel plates Pi, P2. After emerging from the electric field the rays may be taken, to a first order of approximation, as radiating from a virtual source Z half way through the field on the line Si S2. A group of these rays is now selected by means of the diaphragm D, and allowed to pass between the parallel poles of a magnet. For simplicity the poles are taken as circular, the field between them uniform and of such sign as to bend the rays in the opposite direction to the foregoing electric field.
If θ and φ be the angles (taken algebraically) through which the selected beam of rays is bent by passing through fields of strength X and H, then
- (1)
and
- (2)
where l, L are the lengths of the paths of the rays in the fields. Equation (1) is only true for small angles, but exact enough for practice. It follows that over the small range of d selected by the diaphragm θv and φv are constant for all rays of given e/m, therefore
- ,
and
- ,
so that
- ,
when the velocity varies in a group of rays of given e/m.
In order to illustrate in the simplest possible way how this relation may be used to obtain focussing, let us suppose the angles (exaggerated in the diagram) small and the magnetic field acting as if concentrated at the centre O of the pole pieces. If the breadth ZO = b, the group selected will be spread out to a breadth bδθ at O, and at a further distance r the breadth will be
- or . . (3)
Now as the electric and magnetic deflexions are in opposite directions, θ is a negative angle. Say θ = -θ' . Then if φ > 2θ', the quantity (3) will vanish at a value of r given by
- ,
This equation appears correct within practical limits for large circular pole-pieces.
Referred to axes OX, OY the focus is at r cos (φ-2θ'), r sin (φ-2θ') or r,b.2θ'; so that to a first-order approximation, whatever the fields, so long as the position of the diaphragm is fixed, the foci will all lie on the straight line ZF drawn through Z parallel to OX. For purposes of construction G the image of Z in OY is a convenient reference point, φ being here equal to 4θ'. It is clear that a photographic plate, indicated by the thick line, will be in fair focus for values of e/m over a range large enough for accurate comparison of masses.
34. Optical analogue

B, Discharge Tube. A. Anode connected to high potential terminal of induction coil below table. C. Reservoir containing gas to be analysed. I1, I2 Charcoal-liquid air tubes exhausting slit-system and camera. .S. Soft iron plates to shield discharge from stray magnetic field. L. Leads from high tension battery to electric plates. M Du Bois electromagnet. T, Pea lamp for photographing fiducial spot. V, Vacuum-tight and light-tight control for moving photographic plate. W. Camera showing light-tight cap on the left. H, Magnet circuit ammeter. O, Magnet circuit control resistances. G. Gaede rotating mercury pump connected to the camera and the discharge tube by glass tubes and stopcocks.
It may be a help to form an understanding of the principle of the apparatus if we suppose that the beam is one of white light and the electric and magnet fields are glass prisms deflecting the light in opposite directions. The slit system acts as a collimator. If the glass of the first prism has a coefficient of dispersion double that of the second the heterogeneity of the rays of light will cause a spreading of the beam identical with that caused by heterogeneity (in respect to velocity) in the case of the positive rays. It will be clear that if we make the angle of refraction of the second prism more than double that of the first an achromatic image will appear at F.
Since it is a close analogue of the ordinary spectrograph and gives a "spectrum " depending upon mass alone the instrument is called a "mass-spectrograph" and the spectrum it produces a "mass-spectrum." It possesses one notable advantage over the optical spectrograph for, although we can never change the ratio of the dispersions, we can make the refractions whatever we will by the control of X and H, and so bring any desired range of the spectrum on to the plate.
35. The Discharge Tube.
Fig. 9 is a rough diagram of the arrangement of the mass-spectrograph when used for analysing positive rays generated by the ordinary discharge tube method. The discharge-tube B is an ordinary X-ray bulb 20 cm. in T diameter. The anode A is of aluminium wire 3 mm. thick surrounded concentrically by an insulated aluminium tube 7 mm. wide to protect the glass walls, as in the Lodge valve.
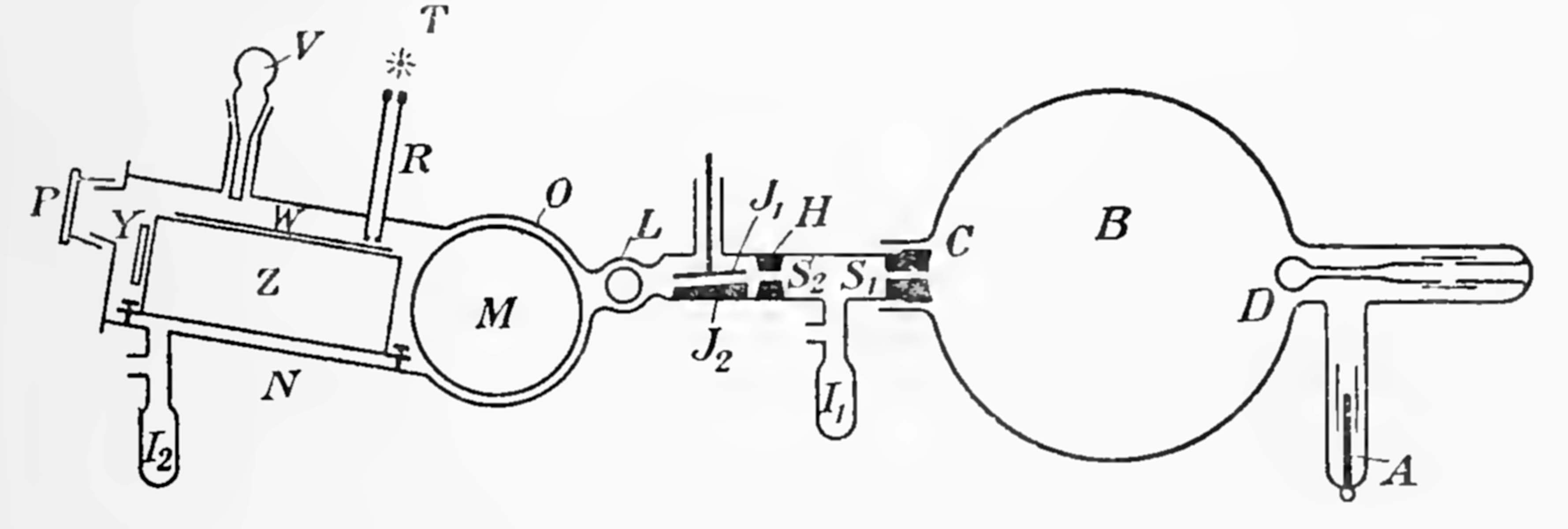
The aluminium cathode C, 2-5 cm. wide, is concave, about 8 cm. radius of curvature, and is placed just in the neck of the bulb this shape and position having been adopted after a short preliminary research.[3] In order to protect the opposite end of the bulb, which would be immediately melted by the very concentrated beam of cathode rays, a silica bulb D about 12 mm. diameter is mounted as indicated. The use of silica as an anticathode has the great advantage of cutting down the production of undesirable X-rays to a minimum. The cathode is earthed.
The discharge is maintained by means of a large induction coil actuated by a mercury coal-gas break; about 100 to 150 watts are passed through the primary, and the bulb is arranged to take from 0.5 to 1 milllampere at potentials ranging from 20,000 to 50,000 volts. Owing to the particular shape and position of the electrodes, especially those of the anode, the bulb acts perfectly as its own rectifier.
The method of mounting the cathode will be readily seen from Fig. 10, which shows part of the apparatus in greater detail. The neck of the bulb is ground off short and cemented with wax to the flat brass collar E, which forms the mouth of an annular space between a wide outer tube F and the inner tube carrying the cathode. The concentric position of the neck is assured by three small ears of brass not shown. The wax joint is kept cool by circulating water through the copper pipe shown in section at G.
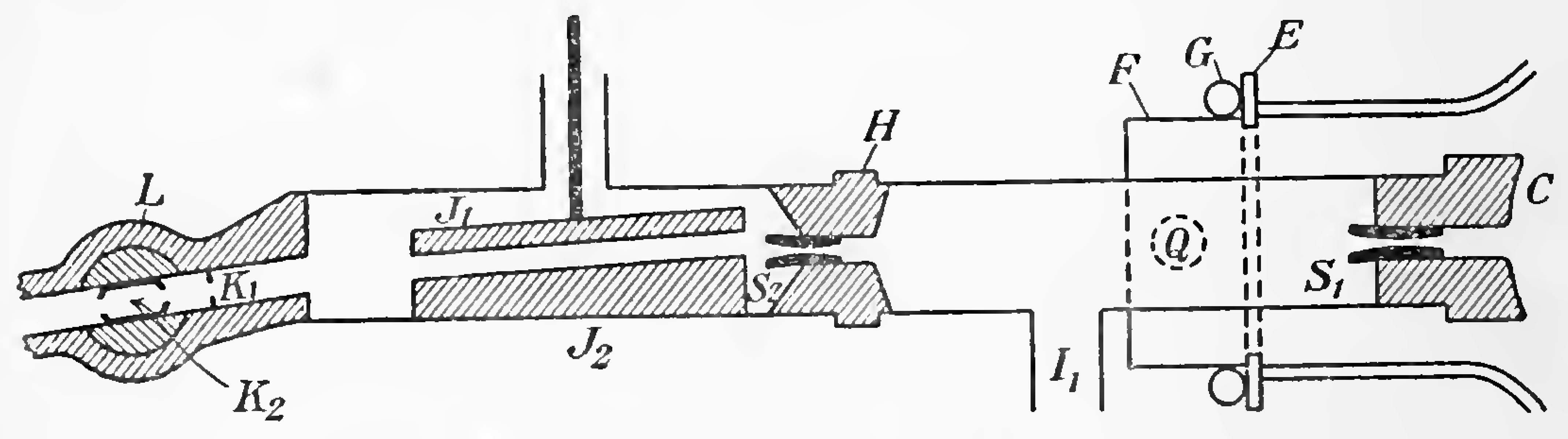
The gas to be analysed is admitted from the fine leak into the annular space and so to the discharge by means of the side-tube attached to F shown in dotted section at Q. Exhaustion is performed by a Gaede mercury-pump through a similar tube on the opposite side. The reason for this arrangement is that the space behind the cathode is the only part of the discharge bulb in which the gas is not raised to an extremely high potential. If the inlet or outlet is anywhere in front of the cathode, falling special guards, the discharge is certain to strike to the pump or the gas reservoir. Such special guards have been made in the past by means of dummy cathodes in the bore of the tubes, but, notwithstanding the fact that the gas can only reach the bulb by diffusion, the present arrangement is far more satisfactory and has the additional advantage of enabling the bulb to be dismounted by breaking one joint only.
36. The Slit System.
The very fine slits used in this apparatus were made with comparative ease as follows: A cylinder of pure aluminium about 10 mm. long by 5 mm. wide is carefully bored with a hole 1 mm. diameter. The resulting thick-walled tube is then cleaned and crushed with a hammer on an anvil until the circular hole becomes a slit about -3 mm. wide. Continuation of this treatment would result in a slit as fine as required giving the maximum resistance to the passage of gas, but its great depth would make the lining up of a pair a matter of extreme difficulty. The crushed tube is therefore now placed between two V-shaped pieces of steel and further crushed between the points of the V's at about its middle point until the required fineness is attained. Practice shows that the best way of doing this is to crush until the walls just touch, and then to open the sHt to the required width by judicious tapping at right angles to that previously employed. With a little care it is possible to make sHts with beautifully parallel sides to almost any degree of fineness, .01 mm. being easily attainable. At this stage the irregularly shaped piece of aluminium is not suited to accurate gas-tight fitting ; it is therefore filled with hard paraffin to protect it from small particles of metal, etc., which if entering cannot be dislodged owing to its shape, and turned up taper to fit the standard mountings. After turning, the paraffin is easily removed by heat and solvents. The centre of the cathode is pierced with a 3 mm. hole, the back of which is coned out to fit one of the standard slits Si. The back of the cathode is turned a gastight fit in the brass tube 2 cm. diameter carrying it, the other end of which bears the brass plug H which is also coned and fitted with the second slit Sa- The two slits, which are roughly .05 mm. wide by 2 mm. long, can be accurately adjusted parallel by means of their diffraction patterns. The space between the sUts, which are about 10 cm. apart, is kept exhausted to the highest degree by the charcoal tube Ii. By this arrangement it will be seen that not only is loss of rays by collision and neutralisation reduced to a minimum but any serious leak of gas from the bulb to the camera is eliminated altogether.
37. The Electric Field
The spreading of the heterogeneous ribbon of rays formed by the slits into an electric spectrum takes place between two parallel flat brass surfaces, Ji, Ja, 5 cm. long, held 2-8 mm. apart by glass distance-pieces, the whole system being wedged immovably in the brass containing-tube in the position shown. The lower surface is cut from a solid cyUnder fitting the tube and connected to it and earth. The upper surface is a thick brass plate, which can be raised to the desired potential, 200-500 volts, by means of a set of small storage-cells. In order to have the plates as near together as possible, they are sloped at 1 in 20 — i.e. half the angle of slope of the mean ray of the part of the spectrum which is to be selected by the diaphragms. Of these there are two: one, K1, an oblong aperture in a clean brass plate, is fixed just in front of the second movable one, K2, which is mounted in the bore of a carefully ground stopcock L. The function of the first diaphragm is to prevent any possibility of charged rays striking the greasy surface of the plug of the stopcock when the latter is in any working position. The variable diaphragm is in effect two square apertures sliding past each other as the plug of the stopcock is turned, the fact that they are not in the same plane being irrelevant. When the stopcock is fully open as sketched in Fig. 10 the angle of rays passing is a maximum, and it may be stopped down to any desired extent by rotation of the plug, becoming zero before any greasy surface is exposed to the rays. Incidentally the stopcock serves another and very convenient use, which is to cut off the camera from the discharge tube, so that the latter need not be filled with air each time the former is opened to change the plate.
38. The Magnetic Field
After leaving the diaphragms the rays pass between the pole-pieces M of a large Du Bois magnet of 2500 turns. The faces of these are circular, 8 cm. diameter, and held 3 mm. apart by brass distance-pieces. The cylindrical pole-pieces themselves are soldered into a brass tube O, which forms part of the camera N. When the latter is built into position, the pole-pieces are drawn by screwed bolts into the arms of the magnet, and so form a structure of great weight and rigidity and provide an admirable foundation for the whole apparatus. Current for the magnet is provided by a special set of large accumulators. With a potential of 300 volts on the electric plates the hydrogen lines are brought on to the scale at about 0.2 ampere, and an increase to 5 amperes, which gives practical saturation, only just brings the singly-charged mercury lines into view. The discharge is protected from the stray field of the magnet by the usual soft iron plates, not shown.
39. The Camera
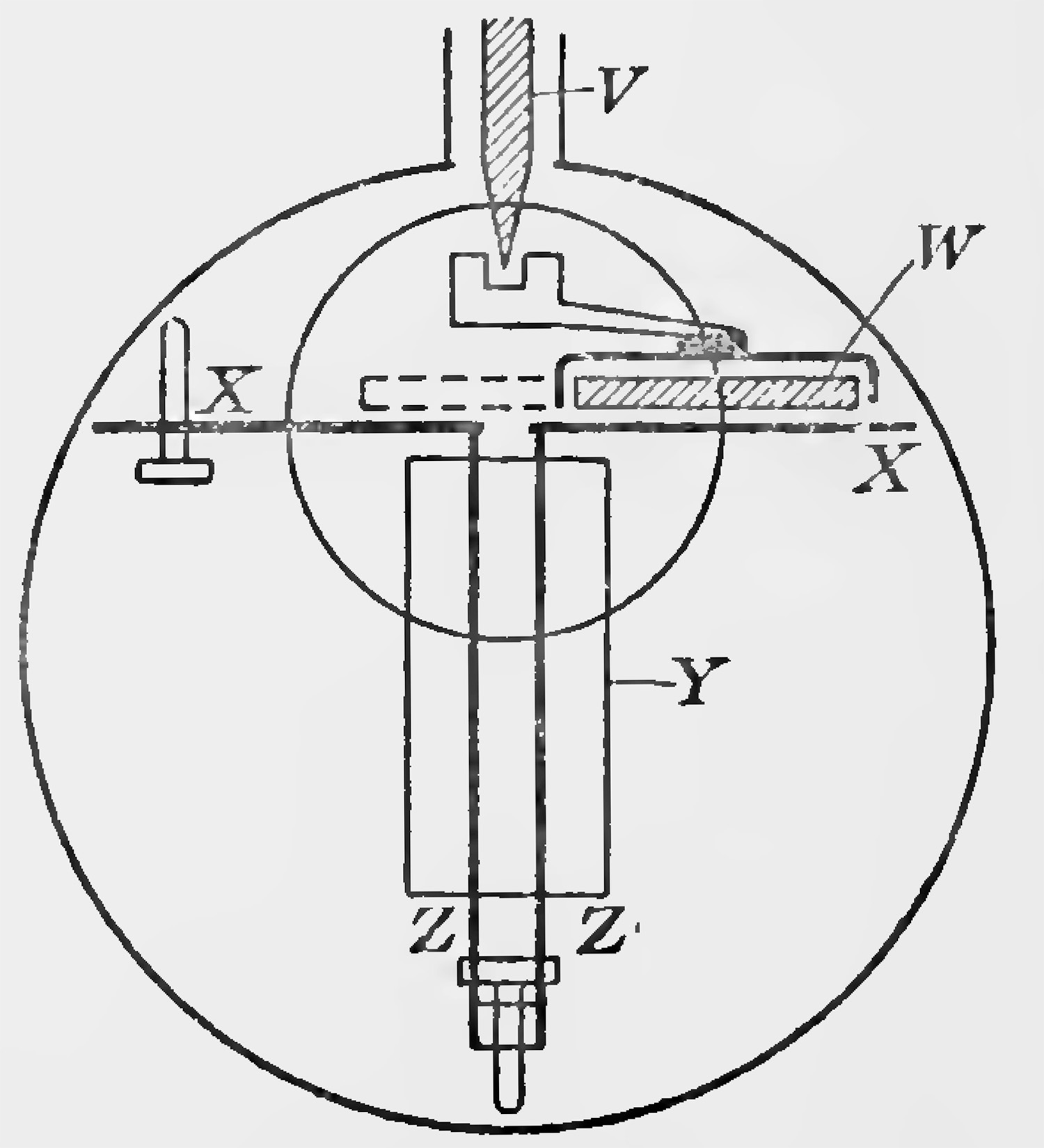
The main body of the camera N is made of stout brass tube 6-4 cm. diameter, shaped to fit on to the transverse tube 0 containing the pole-pieces. The construction of the plate-holder is indicated by the side view in Fig. 9 and an end-on view in Fig. 11. The rays after being magnetically deflected pass between two vertical earthed brass plates Z, Z about 3 mm. apart, and finally reach the photographic plate through a narrow slot 2 mm. wide, 11-8 cm. long, cut in the horizontal metal plate X, X. The three brass plates forming a T-shaped girder are adjusted and locked in position by a set of three leveling-screws, at each end ; the right-hand upper one is omitted in Fig. 11. The plates Z, Z serve to protect the rays completely from any stray electric field, even that caused by the photographic plate itself becoming charged until within a few millimetres of their point of impact.
The photographic plate W, which is a 2 cm. strip cut lengthwise from a 5 x 4 plate, is supported at its ends on two narrow transverse rails which raise it just clear of the plate X, X. Normally it lies to the right of the slot as indicated, and to make an exposure it is moved parallel to itself over the slot by means of a sort of double lazy-tongs carrying wire claws which bracket the ends of the plate as shown. This mechanism, which is not shown in detail is operated by means of a torque rod V working through a ground glass joint. Y is a small willemite screen.
The adjustment of the plate-holder so that the sensitised surface should be at the best focal plane was done by taking a series of exposures of the bright hydrogen lines with different magnetic fields on a large plate placed in the empty camera at a small inclination to the vertical. On developing this, the actual track of the rays could be seen and the locus of points of maximum concentration determined. The final adjustment was made by trial and error and was exceedingly tedious, as air had to be admitted and a new plate inserted after each tentative small alteration of the leveling-screws.
40. Experimental procedure
The plate having been dried in a high vacuum overnight, the whole apparatus is exhausted as completely as possible by the pump with the stopcock L open. Ii and I2 are then cut off from the pump by stopcocks and immersed in liquid air for an hour or so. The electric field, which may range from 200 to 500 volts, is then applied and a small current passed through the magnet sufficient to bring the bright hydrogen molecule spot on to the willemite screen Y, where it can be inspected through the plate-glass back of the cap P, In the meantime the leak, pump, and coil, have all been started to get the bulb into the desired state.
When this has become steady, Jj is earthed to prevent any rays reaching the camera when the plate is moved over the slot to its first position, which is judged by inspection through P with a non-actinic lamp. The magnet current having been set to the particular value desired and the diaphragm adjusted, the coil is momentarily interrupted while Jj is raised to the desired potential, after which the exposure starts. During this, preferably both at the beginning and the end, light from a lamp T is admitted for a few seconds down the tube R (Fig. 9) the ends of which are pierced with two tiny circular holes. The lower hole is very close to the plate, so that a circular dot or fiducial spot is formed from which the measurements of the lines may be made.
The exposures may range from 20 seconds in the case of hydrogen lines to 30 minutes or more, 15 minutes being usually enough. As soon as it is complete the above procedure is repeated, and the plate moved into the second position. In this way as many as six spectra can be taken on one plate, after which L is shut, I2 warmed up, and air admitted to the camera. The cap P, which is on a ground joint, can now be removed, and the exposed plate seized and taken out with a special pair of forceps. A fresh plate is now immediately put in, P replaced and the camera again exhausted, in which state it is left till the next operation.
41. Form of the Spectrum Lines
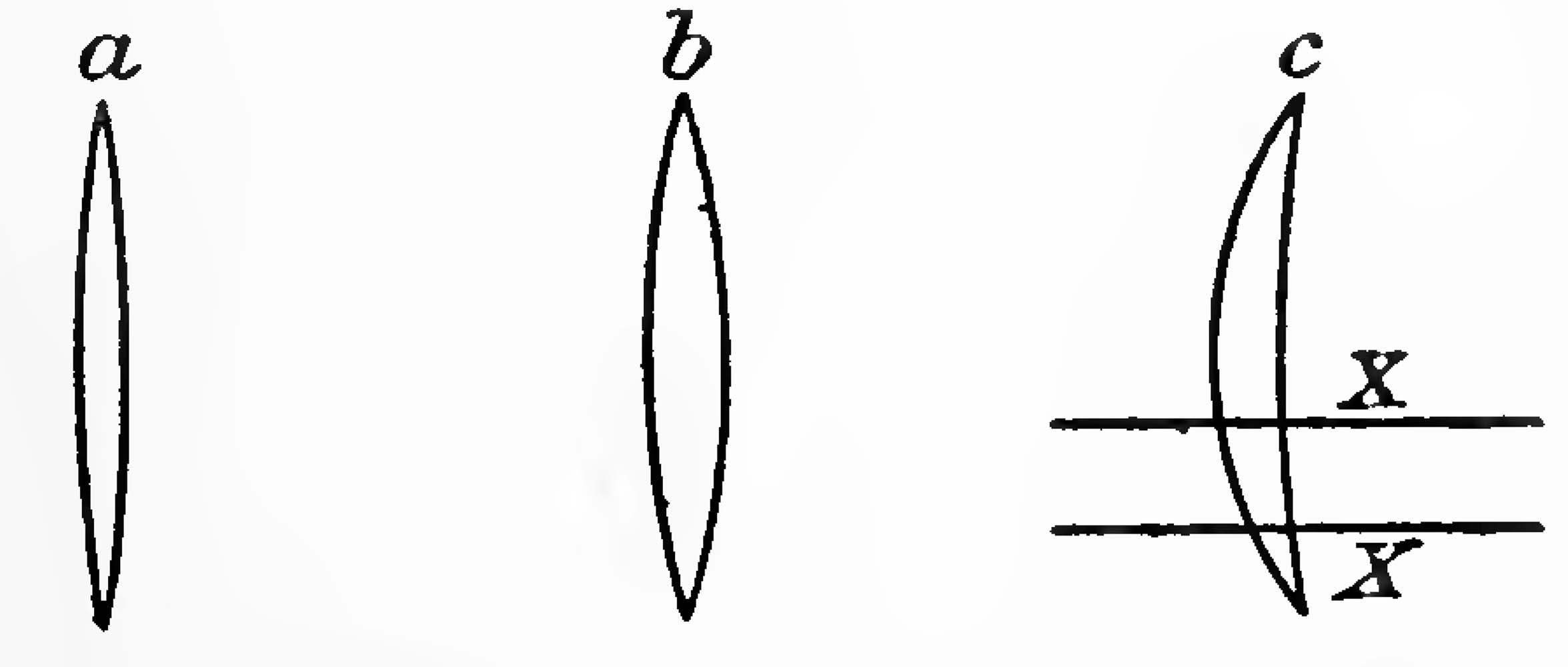
Owing to the form of the slits used, the shape of the spot formed when undeflected rays from such a sht system strike a photograph surface normally, is somewhat as indicated at a (Fig. 12). When they strike the plate obliquely the image would be spread out in one direction, as in b. This would be the actual form in the apparatus, if the deflexions of the mean and extreme rays (i.e., the rays forming the centre and the tips) were identical. This is true of the magnetic field since each cuts the same number of lines of force ; but it is not so in the case of the electric deflexion. Owing in part to the fact that the plates J1, J2 are rectangular and in part to the stray field between the charged plate Ji and the earthed tube in which it is mounted, the extreme rays passing diagonally will be deflected more than the mean rays and the spot bent into the form shown at c. The convex side will be in the direction of the magnetic deflexion, as this is opposed to the deflexion causing the bend. The image on the plate will therefore be the part of this figure falling on the narrow slot in X, X; and as the apparatus is not exactly symmetrical, its shape in the spectra is the figure lying between the lines X, X in Fig. 12, c.
42. The distribution of the mass-spectrum over the photographic plate
In order to study the positions of the focus F (Fig 8) on the plate corresponding to different values of the effective mass m when X and H are constant, we may assume perfect focussing and only consider a single median ray. If R is the radius of curvature of the path of a ray of effective mass m while in the magnetic field, and d the radius of the field, clearly tan ½φ = d/R. But X and θ are constant, hence mv2 must be constant so that the radius of curvature in the magnetic field varies as √m. We may therefore write
- . . . (4)
where m0 is a constant and can be interpreted as that mass which under the conditions of the experiment is bent through a right angle in the magnetic field.
Again if ON the length of the perpendicular dropped from the centre of the magnetic field upon ZF = P (a constant) then
- . . . (5)
By combining (4) and (5) we get an expression for NF/p in terms of m0 and m. This is complicated,[4] but its differential can be shown to vanish when tan ½φ = tan 2θ Thus the mass-scale is approximately linear near ;φ = 4θ
This linear law was observed experimentally at the very outset and though at the time it was unexplained it added greatly to the ease and accuracy of the determinations of m.
The quantity actually measured is the distance between a fixed point on the photographic place called the "fiducial spot"[5] and the focussed image F. Let us call this distance D. D and NF differ by a constant k — about 5.4 cm. in the present apparatus — so that the relation between D and m has the form D = f = (m/m0) where f is a function in which all the coefficients p, k, and tan 2θ are geometrical constants, the fields only affect m0. It follows directly that so long as the apparatus is rigid: If D1 and D2 are the distances from the fiducial spot of any two points on the plate and m0 and m, the corresponding masses for given values of D1 and D2, the ratio m1/m2 will be the same in every photograph.
43. Practical method of deducing the effective mass of a particle from the position of its line on the photograph
The mathematical investigation described above is of interest as it explains the results obtained, but the actual determination of masses from mass-spectra is a purely empirical process, and consists in the comparison of the positions of the Unes caused by the masses in question with the positions of known reference lines. The only assumption made was that given at the end of the previous paragraph and even this was capable of verification by experiment, using such methods as that described on p. 57, or even more fundamentally, in the special case of the ratio 2/1, by the known identity of the mass ratios O2/O, O/O++, and C/C++.
The reference fines used at the outset of the work were lines given by particles of elements and compounds the relative masses of which were known to at least the order of accuracy aimed for. The procedure was somewhat as follows. A series of spectra were taken with say a mixture of CO2 and CH4 in the discharge tube. Previous experience with the parabola method of analysis led to the expectation that lines at 6-C++ , 8-O++ +, 12-C, 16-O, 28-CO, 32-O2, 44-CO2 would certainly be present, there would also be a series of hydrocarbon lines between 12 and 16, CH, CH2, CH3 which could be regarded as known. A spectrum was selected containing as many as possible of these known lines and their masses m1, m2, m3 were plotted against the distances of the lines from the fixed fiducial spot and a curve drawn through the points so obtained. This is our first calibration curve of necessity inaccurate owing to the gaps between the points. A second spectrum was now taken in which the same fines appeared in a different place, for by altering the magnetic field we can place them wherever we please, and the new set of distances from the fiducial spot measured. These distances were now transformed into masses (no longer integral) m1', m2', m3', by means of the curve previously drawn. Supposing the curve to be accurate and the ratio law to hold
where r is clearly a measure of the change in m0 in the mathematical discussion above. In practice these ratios were found to be very nearly the same, so that a mean value of r could be taken with confidence. The known masses multiplied by that mean now gave a new set of points on the original curve. By carrying on this process all the serious gaps in the curve could be bridged and its accuracy brought up to the required standard.
The calibration curve so formed renders the identification of one fine sufficient to deduce the masses corresponding to all the other lines on the plate, and as in general many lines are known on each spectrum, its accuracy is continually subject to fresh test. In practice it was found perfectly reliable so long as none of the geometrical constants of the apparatus were altered.
Owing to the linear relation at φ = 2θ the actual curve was very nearly straight for a considerable portion of its length. This allowed the following alternative procedure to be adopted if desired. A linear relation was assumed and a table of corrections made by means of reference lines, and these corrections when subtracted from the observed displacements gave an exactly linear relation with mass. A correction-curve (apparently parabolic) was drawn, from which the appropriate correction for any displacement could be written down and the mass corresponding to this displacement obtained by simple proportion.
In connection with the use of reference lines it might be thought difficult to know which of the lines on a plate corresponds to a known mass, since they are not labelled in any way. A little consideration will show that the same difficulty is raised in the case of the standard lines of the iron arc and the stars in the sky, yet neither the spectroscopist nor the astronomer have the least difficulty in recognising enough for their purpose, indeed a mistake in identity would lead in most cases to an error so gross as to compel immediate attention. This comparison is perhaps a little flattering to the lines on a mass-spectrum as these alter their relative intensity to some extent, but in particular cases, such as those of the hydrocarbons and mercury, identification is, after a little experience, as easy as that of the Pole Star or of the D lines in the spectrum of sodium.
44. Comparison of masses by the method of "coincidence"
The method of deducing the masses of particles from the position of their lines described in the foregoing paragraph is simple and straightforward. It also has the great advantage of not requiring an accurate knowledge of the numerical values of the electric and magnetic fields. The only requisite is that these should be constant during the exposure, and even if this constancy is not quite perfect the shift in position will affect all the lines known and unknown alike and therefore introduce no serious error into the results obtained. There is, however, another method of comparing masses which requires no knowledge, either theoretical or empirical, of the relation between effective mass and measured displacement. This is independent of the calibration curve and therefore constitutes a valuable check on results obtained by its use. It depends upon the following considerations: Suppose we wish to compare an unknown mass m' with a known mass m. A mass-spectrum is taken with fields X and H such that the mass m gives a fine at a certain position on the plate. The fields are now altered until the line caused by the unknown mass m' is brought to the identical position on the plate previously occupied by the fine due to m. The paths of the rays in the two cases must be identical, hence if X', H' are the new values of the fields it follows at once from equations (1) and (2)[6] that
- .
Now it is only necessary to measure one of the fields if we keep the other constant and therefore H, which cannot be measured or reproduced accurately, is kept constant, and X is measured. For the latter purpose it is only necessary to measure the potentials applied to the plates P1, P2, which can be done with the greatest ease and accuracy.
Thus, to take a numerical illustration, the position occupied by the line due to carbon (12) with a potential on the plates of 320 volts should be exactly coincident with that occupied by the line due to Oxygen (16) with 240 volts when the magnetic field is kept constant. All such coincidences have so far been found to occur within the error of experiment, whatever the position on the plate.
Methods depending on the measured variation of X with H constant have some practical disadvantages. The first and most obvious of these is that any small change in the value of the magnetic field between the two exposures will lead to a definite error, this error will be double the percentage change in the field, since the square of the latter is involved. The second objection is founded on considerations of intensity. If the parabola method of analysis is compared with the mass-spectrograph it will readily be observed that, in effect, the latter focusses at a point all the rays which in the former method form a short element of arc on a parabola. The length of the element of arc is determined by the angle of the electric spectrum allowed to pass, i.e. the width of the diaphragm. Its position on the parabola is at our disposal, for, referring to Fig. 4, p. 28, it wiU be seen that the higher we make X, that is to say the higher the energy of the beam of rays we select at constants, the nearer the element of arc will approach the axis OY, in fact its distance from that axis will simply be inversely proportional to X. Also, however many parabolas we consider and however much we move them about by changing H, so long as X is constant the elements of arc selected will all he on a line parallel to OY. Now it has already been pointed out[7] that the intensity of normal parabolas is a maximum near the head p, where the energy corresponds to the full fall of potential across the discharge tube, and fades away rapidly, in some cases very rapidly indeed, at points more distant from the origin. In order to get the greatest intensity at the focussed spot we must therefore choose X so that the element of arc selected will be near the head of the parabola. This is done in practice by observing visually, by means of a willemite screen, the very bright Une given by the hydrogen molecule while different potentials are apphed to the plates. The best value of X so determined must also be the best value for all the other normal lines, so that in the ordinary calibration curve method, when X is kept constant, it is possible to use conditions in which all the normal lines on the mass-spectra will be at their brightest together, whatever range we bring on to the plate by altering the magnetic field.
In the coincidence method this very fortunate circumstance cannot be taken advantage of, for with H constant the selected elements of arc will now lie on a line parallel to OX. We can only arrange matters for one, the lighter, of the two masses to be compared, to be at its optimum. In the case of the heavier the selected arc must he at a greater distance from the origin and therefore provide a much feebler intensity. The disparity in brightness, due to this effect will be the greater the greater the ratio of the masses considered; it can be corrected to some degree by softening the discharge tube while the heavier mass is being photographed.
In spite of these drawbacks the principle underlying the coincidence method is probably the most suitable for massratio measurements of the highest accuracy. The fact that the paths of the rays is the same in the case of both masses eliminates all errors due to non-uniformity of the fields and the results are independent of any assumptions as regards the ratios of the reference lines themselves. It is the only method at present available in the case of elements far removed, on the mass-scale, from the reference lines, and a modification of it called the method of "bracketing" has been successfully used to evaluate the masses of helium and hydrogen.[8]
45. The measurement of the lines
The accurate determination of the distance of the lines from the fiducial spot is a physical problem of considerable interest. The image itself is due to a caustic of rays, the edge of which will be sharp on the side of maximum magnetic displacement, so that this, the left side in the Plates, may be expected to maintain its sharpness when a large diaphragm is in use, while the other will fade away gradually. Hence very bright lines will be broadened to the right by this effect (which is analogous to spherical astigmatism in ordinary lenses), but to the left the only broadening will be that due to ordinary halation. The relative importance of these two forms of spreading can be gauged by taking photographs with a very small diaphragm, for then the first will be eliminated and the second can be estimated by comparing lines of different intensity. It is found that for ordinary diaphragm apertures the halation effect is much the smaller; it can also be minimised by using lines of approximately equal intensity so that the most reliable measurements of lines for position are obtained from their left-hand edges. This is well illustrated in the " bracketed " lines of hydrogen a and c, Plate III. In {a) measurements of the left hand side of the three lines shows this bracket to be really symmetrical though it does not appear so to the eye, on account of the astigmatic spreading of the middle line caused by the use of an open diaphragm and rather too long an exposure. In (c) the diaphragm was almost closed and the exposures more carefully adjusted, so that both sides of the lines are sharp and their breadths practically identical.
The most accurate measurements were made on a comparator. The spectrum was set as closely as possible parallel to the axis of the instrument, and the distances between the left-hand edge of the lines and the fiducial spot read off on a Zeiss standard scale. For faint lines it was necessary to use a very low power eyepiece of the reading microscope, and in the case of the faintest lines of all, the best results could be obtained by laying a millimetre scale on the plate and estimating the distance from the fiducial spot to the optical centre of the lines, by the unaided eye.
46. Resolving power and accuracy of mass determinstion
Taking the width of the slits as 1/25 mm. and putting in the dimensions of the present apparatus the theory shows that in the region φ = 4θ lines differing by a little less than 1 per cent, should be just separated. In actual practice a better result was obtained, for the instrument is capable of separating the lines of xenon, which differ by 1 in 130 ; this is probably because the part of the line which falls on the strip of plate exposed is due to the narrower edges of the slits.
The numerical relation between mass and position in this part of the spectrum corresponds to a shift of 1.39 mm. for a change of mass of 1 per cent., so that even with the unaided eye an accuracy of 1 part in 1,000 can be approached. Although it is sufficient in theory to know the mass of one Hne only to determine, with the calibration curve, the masses of all the others, in practice every effort is made to bracket any unknown line by reference lines and only to trust comparative measurements when the lines are fairly close together. Under these conditions an accuracy of 1 in 1,000 is claimed and there is httle doubt that in favourable cases it is exceeded.
47. Order of results and nomenclature
In the descriptions of the results obtained with the mass-spectrograph contained in the following chapters the order of the elements given is, when possible, that in which the experiments were made. There is a practical reason for this procedure, as in most cases it was impossible to eliminate any element used before the following one was introduced. Evacuation and washing have little effect, as the gases appear to get embedded in the surface of the discharge bulb and are only released very gradually by subsequent discharge.
The problem of nomenclature of the isotopes became serious when the very complex nature of the heavy elements was apparent. It has been decided for the present to adopt the rather clumsy but definite and elastic one of using the chemical symbol of the complex element, with an index corresponding to its mass : e.g. Ne22 Rb87 This system is made reasonable by the fact that the constituents of complex elements have all so far proved to have masses expressible in whole numbers.
48. Lines of the First, Second and higher Orders
It was shown on page 30 that particles having two charges gave a parabola corresponding to an effective mass of one hah the normal mass. In the same way a particle with three charges wiU have an effective mass of one third, and so on.
These apparent masses will duly make their appearance on mass-spectra as lines corresponding to simple fractions of the real mass causing them. It is convenient in these cases to borrow the nomenclature of optics and refer to the Unes given by singly, doubly, and multiply charged particles respectively as Unes of the first, second, and higher orders. Thus the molecule of oxygen gives a first order fine at 32, and its atom first and second order lines at 16 and 8.
The empirical rule that molecules only give first order lines[9] is very useful in helping to differentiate between atoms and compound molecules of the same apparent mass. Some results given below,[10] however, show that in certain cases it breaks down, so that inferences made from it must not be taken as absolutely conclusive.
49. Negative mass-spectra
It has been mentioned that positive rays could become negatively charged by the capture of electrons by collisions in the narrow canal-ray tube of the Thomson apparatus, and so produce parabolas in the quadrant opposite to that containing the normal ones. The sHt system of the mass-spectrograph is specially designed to eliminate such collisions as far as possible by exhausting the space between the slits. If the means of exhaustion of this space is deliberately cut off, and the normal electric and magnetic fields both reversed in sign it is possible, at a small cost in definition of the lines, to photograph the mass-spectra of negatively charged particles. Such negatively charged particles are only formed by elements or compounds having marked electronegative properties. Very little work has been done in this interesting field, but certain ambiguities in the interpretation of the chlorine results have been satisfactorily cleared up by its means.
References
Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.
