Aston 1922/Chapter 8
Chapter VIII - The Electrical Theory of Matter
Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.
84. The Whole Number rule
By far the most important result of the measurements detailed in the foregoing chapters is that, with the exception of hydrogen, the weights of the atoms of all the elements measured, and therefore almost certainly of all elements, are whole numbers to the accuracy of experiment, in most cases about one part in a thousand. Of course, the error expressed in fractions of a unit increases with the weight measured, but with the lighter elements the divergence from the whole number rule is extremely small.
This enables the most sweeping simplifications to be made in our ideas of mass, and removes the only serious objection to a unitary theory of matter.
85. The Unitary Theory of the constitution of matter
From the very earhest times it has been a favourite hj'pothesis that all matter is really composed of one primordial substance, Air, Fire, Earth and Water have all been suggested in the past. The first definite theory of the constitution of the atoms of the elements out of atoms of a primordial element (Protyle, Urstoff, etc.) was made by Prout in 1815. Prouts Hypothesis was that the atoms of the elements were different aggregations of atoms of hydrogen. On this view it is obvious that the atomic weights should all be expressed by whole numbers when the atomic weight of hydrogen itself is taken as unity. Owing to the roughness of the methods available and the considerable inaccuracies of the atomic weight determinations made at that time there was little to disprove the hypothesis, and its marked simplicity gained it many adherents. But as time went on chemical methods grew more precise and it became more and more impossible to reconcile experimental results with integral combining weights until the evidence against it was strong enough to cause J. S. Stas (1860-1865) to state: "I have arrived at the absolute conviction, the complete certainty, so far as it is possible for a human being to attain to certainty in such matters, that the law of Prout is nothing but an illusion, a mere speculation definitely contradicted by experience."
Nevertheless, though abandoned temporarily by the chemist as impracticable, the idea of primordial atoms appealed strongly to the mind of the philosopher and the physicist. Herbert Spencer, in his hypothesis of the constitution of matter, says: "All material substances are divisible into so-called elementary substances composed of molecular particles of the same nature as themselves ; but these molecular particles are complicated structures consisting of congregations of truly elementary atoms, identical in nature and differing only in position, arrangement, motion, etc, and the molecules or chemical atoms are produced from the true or physical atoms by processes of evolution under conditions which chemistry has not been able to reproduce."
The discovery of the electron, the proof that it was the same whatever the atom from which it was detached and, most important of all, the demonstration by Sir J. J. Thomson and others that electricity could simulate the known properties of matter, gave us the key to the riddle of what these primordial atoms really are. The only serious obstacle, the fractional atomic weights, has now been removed so that there is nothing to prevent us accepting the simple and fundamental conclusion: The atoms of the elements are aggregations of atoms of positive and negative electricity.
86. The Atom of Negative Electricity, or Electron
The fundamental unit of negative electricity makes its appearance in physical phenomena in many guises, such as the cathode ray of electrical discharge, the beta ray of radioactive change, the thermion of the wireless valve. A very complete account of it has recently been published by Millikan[1] so that it is not proposed to describe its history and properties at any length here. It will be sufficient to note a few of its more important constants.
Its charge e is given by Millikan as 4.774 X 10-10 E.S.U. The most reliable measurements of e/m for the electron, at low velocity, give the value 5.30 x 10-10 E.S.U. Hence its mass is almost exactly 9.00 X 10-28 grs, 1845 times less than the mass of the hydrogen atom, or 0.00054 on the ordinary scale of atomic weights (Oxygen = 16).
87. The atom of Positive Electricity, or Proton
Our physical knowledge of this body is not nearly so complete as that of its counterpart the electron. It is very significant that in no analysis of positive rays so far performed have we been able to discover a particle of mass less than that of the hydrogen atom. This direct result, supported as it is by many less direct lines of evidence, leads logically to the conclusion that the hydrogen positive ray, i.e. the positively charged part remaining when an electron is detached from a neutral hydrogen atom, is the atom of positive electricity itself. The name "proton"[2] was suggested for it by Sir Ernest Rutherford at the Cardiff meeting of the British Association in 1920. The charge on a proton is, of course, equal and of opposite sign to that on the electron. Its mass in the free state has been measured directly[3] and is practically identical with that of the neutral atom of hydrogen 1.66 x 10-24 grs., or 1.007 on the oxygen scale.[4]
88. The Nucleus Atom
Certain experimental results, notably the scattering of alpha rays, led Sir Ernest Rutherford in 1911[5] to formulate an atom model which has resulted in the most remarkable advances in both physics and chemistry, and is now almost universally accepted as correct in fundamental principle. This is that an atom of matter consists of a central massive nucleus carrying a positive charge which is surrounded, at distances relatively great compared with its diameter, by "planetary" electrons. The central nucleus contains all the positive electricity in the atom, and therefore practically all its mass. The weight of the atom and its radioactive properties are associated with the nucleus; its chemical properties and spectrum, on the other hand, are properties of its planetary electrons. It is clear that in a neutral atom the positive charge on the nucleus must be equal to the sum of the negative charges on the planetary electrons.
89. Moseley's Atomic Numbers
The scattering experiments mentioned above indicated that the net positive charge on the nucleus (expressed in terms of the natural unit e) was roughly equal to half the atomic weight. Now if we arrange the elements in order of atomic weight, starting with hydrogen, each element will have a position the number of which will be about half its atomic weight. It was suggested by Van den Broek that this atomic number might be equal to the charge on the nucleus. Two years after the formulation of the nucleus atom theory Moseley undertook an investigation of the changes which took place in the wave-length of the X-rays given off when various elements were used in turn as anticathodes. The result of this piece of work, now classical,[6] was the establishment of the most important generalisation in the history of chemistry since Mendeleef's Periodic Law. Discussing a quantity Q related to wave-length Moseley writes:
"It is at once evident that Q increases by a constant amount as we pass from one element to the next, using the chemical order of the elements in the periodic system. Except in the case of Nickel and Cobalt,[7] this is also the order of the atomic weights. While, however, Q increases uniformly the atomic weights vary in an apparently arbitrary manner, so that an exception in their order does not come as a surprise. We have here a proof that there is in the atom a fundamental quantity, which increases by regular steps as we pass from one element to the next. This quantity can only be the charge on the central positive nucleus, of the existence of which we already have definite proof. Rutherford has shown, from the magnitude of the scattering of a particles by matter, that the nucleus carries a positive charge approximately equal to that of A/2 electrons when A is the atomic weight. Barkla, from the scattering of X-rays by matter, has shown that the number of electrons in an atom is roughly A/2, which for an electrically neutral atom is the same thing. Now the atomic weights increase on the average by about 2 units at a time, and strongly suggest the view that N increases from atom to atom always by a single electronic unit. We are therefore led by experiment to the view that N is the same as the number of the place occupied by the element in the periodic system. This atomic number is then for H 1, for He 2, for Li 3 for Ca 20 for Zn 30, etc. This theory was originated by Broek[8] and since used by Bohr. We can confidently predict that in the few cases in which the order of the atomic weights A clashes with the chemical order of the periodic system the chemical properties are governed by N, while A itself is probably some complicated function of N."
Subsequent work has supported in an unquestionable manner the ideas so expressed by Moseley. That the number of the element in the order of the periodic table is actually the same as the positive charge on the nuclei of its atoms, expressed of course in terms of the natural unit of electric charge e, has been proved by direct experiment for some of the heavier elements. The recent work of Chadwick[9] leaves little room for doubt on that point. At the other end of the scale all the known properties of hydrogen point to the conclusion that its atomic number is 1; its exceptional atomic weight, as will be seen later, is itself strong corroborative evidence of this.
A complete table of the elements with their Atomic Numbers, Atomic Weights and isotopes (where these are known) is given on page 142.
From Moseley's law of atomic numbers the explanation of the empirical rule of radioactive transformation given on page 11 follows at once. An alpha particle carries two positive charges, a beta particle one negative one. If therefore the atom of a radioactive substance emits one alpha particle from its nucleus it naturally descends two units in atomic number, that is moves back two places in the periodic table. If on the other hand it emits one beta particle it clearly moves forward one place, for by the operation the nucleus has acquired one additional charge.
90. The Bohr Atom
In this atom model the electrons outside the nucleus are supposed to be in a state of continual revolution about it, like planets round the sun. This rotation is considered to take place in orbits defined in a very special manner by means of a "quantum relation." This postulates that when, and only when, an electron changes its orbit, radiation is given out and the energy acquired by the change of orbit is entirely given off as radiation of frequency ν where the change of energy equals hν where h is Planck's quantum or element of action (6.55 x 10-22 C.G.S.).[10] This theory lends itself to exact mathematical analysis but unfortunately it can only be worked out adequately for the two simplest cases, the neutral hydrogen atom and the singly charged helium atom. Here, however, its success is most remarkable; for not only is it possible to calculate by its means the wave length of the chief series lines of the hydrogen spectrum, to an accuracy almost unprecedented in physics, but, by applying the relativity correction for change of mass with velocity to the rotating electron, the fine structure of the fines and the effects of electric and magnetic fields have been predicted with the most astonishing exactness by Sommerfeld, Epstein and others.[11] Bohr has recently expressed the hope of extending his theory to heavier atoms by means of a new device which he terms the principle of "correspondence."[12]
91. The Lewis Langmuir Atom
This form of atom model was primarily designed to afford some theoretical basis for the numerous general qualitative properties of elements and their compounds. In it the electrons outside the nucleus are supposed to be at rest at, or vibrating about, definite points. The first two electrons will form a pair, the next eight will tend to set in positions corresponding to the eight corners of a cube, or some other soUd figure, and so on. In this way we shall get a series of shells or sheaths one outside the other. Langmuir has recently[13] reduced his postulates to the following three:
- (1) The electrons in atoms tend to surround the nucleus in successive layers containing 2, 8, 8, 18, 18, 32 electrons respectively.
- (2) The atoms may be coupled together by one or more "duplets" held in common by the complete sheaths of the atoms.
- (3) The residual charge on the atom and on each group of atoms tends to a minimum.
This atom model is not amenable to mathematical treatment, but it has been exceedingly successful in accounting for the general chemical qualitative properties of many of the elements and in predicting those of their compounds.
92. Diagrammatical representation of atoms of Isotopes and Isobares
The accompanying diagrams (Fig. 16) are intended to indicate the sort of arrangements which may take place in atoms. The small dark circle is the nucleus, the number of protons and electrons comprising it being indicated by the numerals. The electrons outside the nucleus are indicated by small Light circles.
(1) is an atom of atomic weight 6. Its nucleus contains 6 protons and 3 electrons, hence its atomic number is 3. It is in fact the atom of the lighter isotope of lithium of atomic weight 6, Li6. To be electrically neutral it must have 3 electrons outside the nucleus. Now the principles underlying Langmuir's first postulate are derived from the Periodic Table and are certainly correct. Langmuir explains this by saying that the first two of these electrons will form an innermost ring or shell of two. This shell being now complete, any more electrons will go outside and start the next shell of eight, so we indicate this by putting the third electron in a circle of greater diameter.
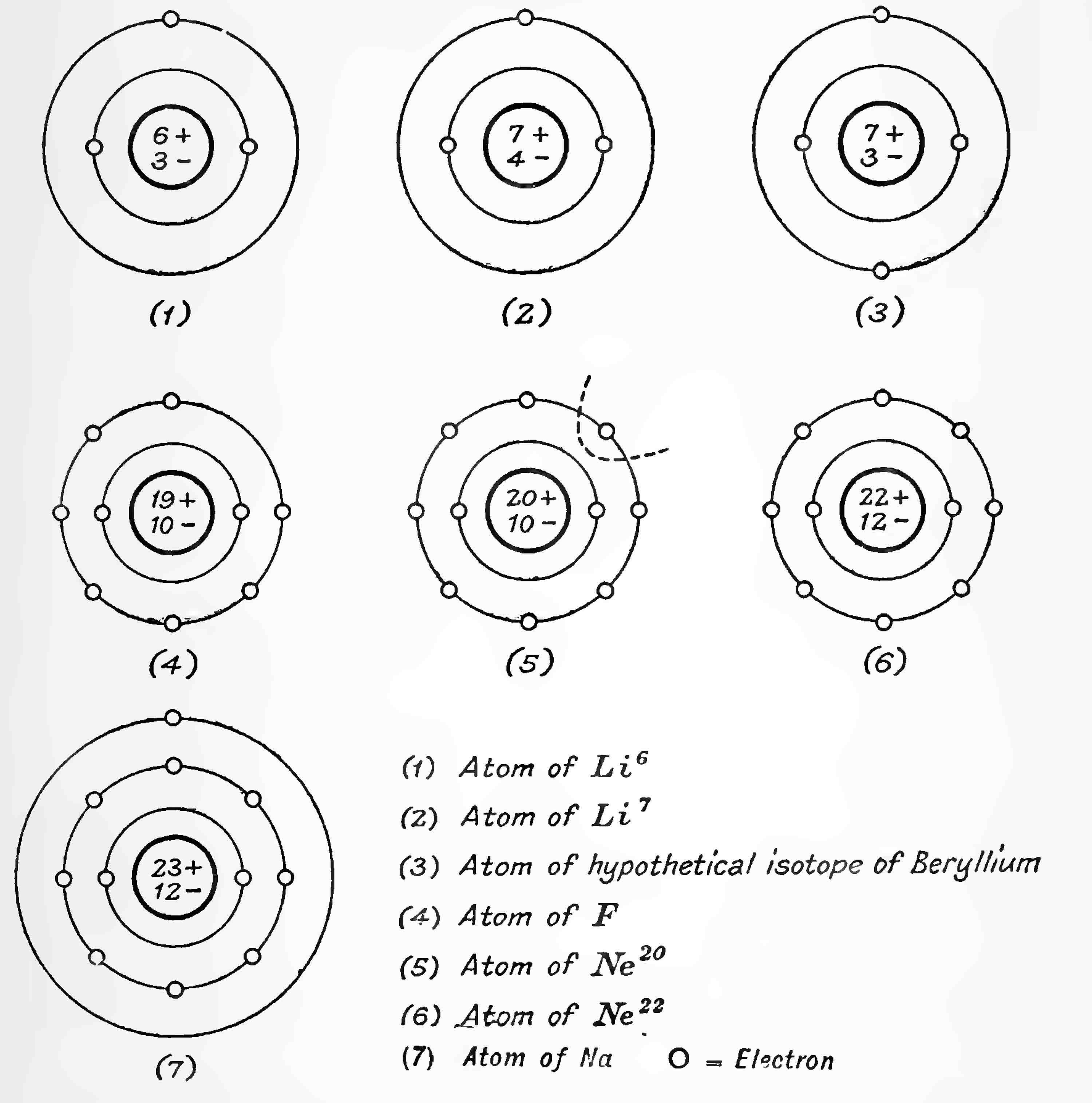
Now suppose we add one electron and one proton to this atom. If both enter the nucleus we shall get the configuration represented by (2) The nuclear charge is unaltered, so that the arrangement of the exterior electrons will be precisely the same. It follows that all properties depending on these electrons such as atomic volume, spectrum, chemical properties, etc., will be quite unaltered. But the weight of this atom is now 7, so it is an isotope of lithium ; it is actually the atom of the heavier constituent Li7. (1) and (2) are Isotopes.
But now suppose we add a proton and an electron to (1) so that the proton only enters the nucleus and the electron remains outside as shown at (3) We shall now have a charge 4 on the nucleus and two electrons in the outer ring. The chemical properties of such an atom, if it could exist, would be completely different from those of Uthium, but would be identical with those of beryllium, of which it would be an isotope. But its mass is clearly identically the same as that of (2) so that (2) and (3) are Isobares.
In the same way (4) will be recognised as the atom of fluorine (5) and (6) as the atoms of the two isotopes of neon and (7) as the atom of sodium.
93. The relation between Isotopes and Elements in the same Group
As far as can be seen the chemical properties by which the elements are divided into groups depend practically entirely on the outermost shell of electrons, which are therefore called valency electrons. Now consider all that part called by Langmuir the kernel of the atom lying within the shell of these valency electrons. The movements or configuration of the outermost electrons will depend in the first degree on the charge on the kernel, which may be looked upon as a virtual nucleus. The kernels of atoms (1) and (7) both have the same net charge 1, so that the elements they represent should have many chemical similarities. These they certainly have as both are alkaU metals. In general the atoms of elements belonging to the same group chemically have the same number of electrons in the outer shell and the same net charge on the kernel. On this view it will be seen that the similarity of isotopes may be regarded as the extreme limiting case of the similarities long observed between elements of the same chemical group.
94. Abnormal compounds formed by charged atoms
The tendency of elements to form compounds with each other, that is the property with which the idea of valency is associated, is ascribed to the tendency of the atom to complete its outer shell. This it can do either by parting with the electrons in this shell and so promoting the next inner completed shell to outer position, or by sharing the electrons in the atom of another element so that they fill the gaps in its own outer shell. We have already alluded to the success which has attended this idea in explaining valency and the properties of chemical compounds. For the present argument it will be enough if it is understood that lithium and sodium (1) (2) (7) will very readily part with their solitary valency electron and become positively charged, i.e., will be strongly electropositive elements with valency +1; whereas a fluorine (4) will have an equally powerful tendency to take up an electron and become negatively charged and so will be a strongly electronegative element with valency 1, Both of these tendencies will be satisfied if (4) and (7) combine forming the compound molecule NaF, for the outer electron of (7) will enter the outer shell of (4) thus forming two complete shells of eight (Langmuir's octets). We trace the tendency of the atom of fluorine, or any other halogen, to form compounds with the atom of an electropositive element, or with the atom of hydrogen, to the fact that it has one too few electrons in its outer shell.
Now the only way we can give a positive charge to an atom of neon (5) or (6) is by knocking one or more electrons out of its outer shell. Suppose we remove one from (5) as indicated by the dotted line. (5) now will have a similar outer shell to (4) and a valency 1, so we may expect that atoms of the inert gases carrying a single positive charge will behave chemically in a similar manner to neutral halogen atoms and will therefore be capable so long as they are charged of forming hydrides. This very important idea was first suggested by Sir J. J. Thomson in connection with the charged atoms of chlorine[14] and certainly supplies a very satisfactory explanation of the very abnormal hydrides of inert gases and compounds such as OH3 discovered in positive rays. The line at 41 (Spectrum VI, Plate III) is probably to be put down to a charged hydride of argon of this type. Exceedingly faint lines at 5 in the case of helium, and 21 in the case of neon, are probably to be ascribed to similar abnormal compound (HeH) and (NeH) respectively. In the case of atoms carrying more than one charge it can be generally stated that each positive charge given to an atom will increase its negative valency by one.
95. The failure of the additive law in respect to mass
We have seen that, for velocities small compared with that of light, the masses of the proton and the electron may be regarded as universal constants. If the additive law were strictly true as regards the summation of their masses it is clear that any mass whatever, whether it were that of an atom or a molecule, a planet or a star, or even the universe itself could be expressed in the form NM where N is a pure integer and M the mass of the neutral system 1 proton +1 electron (= the atom of hydrogen). The simplicity of this idea, which is Prout's theory in the language of modern physics, is extremely attractive; but we know it to be false, for although the discovery of isotopes has removed the difficulty of the grosser fractions associated with such elements as neon and chlorine, we are still left with the more minute but none the less real one associated with hydrogen itself. To explain this the additive law must be qualified by some such reasoning as is contained in the following paragraph.
96. The explanation of the fractional mass of the hydrogen atom by the hypothesis of packing"
According to generally accepted views the proton and the electron possess mass, or what on the relativity theory is regarded as the same thing, weight, by virtue of the energy in the electromagnetical field which surrounds them. It can easily be shown on classical lines that if we give it a spherical form a charge e spread uniformly over the surface of the sphere will have a mass m when its radius a is such that ; hence to give the electron its proper mass its charge must be compressed to a sphere of diameter about 3.8 x lO-13 cm. By the same argument the proton will be nearly two thousand times smaller and have a diameter 2.06 x 10-16 cm. The extreme range of the diameter of atoms themselves is 1 – 5 X 10-8 cm., so that it will at once be realised that the structure of an atom is an exceedingly open one, even more so than that of our solar system.
Now it can be shown that if we bring two charges of opposite sign sufficiently close together their fields will affect each other in such a way that the mass of the system will be reduced. This effect is quite inappreciable for distances comparable with the diameter of an atom, but begins to make itself felt when the distance apart is of the order of the size of the electron itself as given above. The nucleus of the atom of an ordinary element (not hydrogen) contains both protons and electrons and is very small compared with the atom itself. Its dimensions can be roughly determined by actual experiment in the case of the heavy elements and are found to be so small that even to get in the electrons alone these would have to be packed very closely together. Such a nucleus will contain more protons than electrons, roughly twice as many, so that it may be regarded as practically certain that: In the nuclei of normal atoms the packing of the electrons and protons is so close that the additive law of mass will not hold and the mass of the nucleus will be less than the sum of the masses of its constituent charges.
The nucleus of a hydrogen atom consists of one single free proton, its planetary electron is too far away to cause any effect so that it is clear that we shall find the mass associated with the atom of hydrogen greater than one-fourth the mass of a helium atom or one-sixteenth the mass of an oxygen atom. The mass lost when four free protons and two free electrons are packed close together to form a helium nucleus (No. 9, p. 106) is roughly 0.7 per cent, of the whole and it can be calculated that, if we take the value of the diameter of the electron given above, the protons must approach nearer than half of this to give so large a reduction. This means that the charges must be so closely packed that the electrons are actually deformed.
The whole number rule may now be simply translated into a statement that the mean packing effect in all atoms is approximately constant, and the unit of mass 1 when O = 16 will be (mass of a packed proton) (mass of free electron) (mass of packed electron). The whole number rule is not, and never was supposed to be, mathematically exact, for this would imply an identical packing effect in the case of all atoms, an exceedingly improbable supposition. It is almost certain that atoms of some elements, such as nitrogen, weigh slightly more than a whole number (looser packing) while those of others such as caesium or iodine may weigh slightly less (closer packing). The limit of accuracy so far attained in mass-spectrum measurement is not sufficient to detect a change of the order expected, except in the case of hydrogen, where the variation in mass is exceptionally high.
97. The structure of the nucleus
The manner in which the units of electricity are arranged in the nucleus of an atom has received a good deal of attention from theorists but ideas on this subject are almost entirely of a conjectural character. Thus Harkins[15] has proposed a constitutional formula for the nuclei of all the elements. In this, besides electrons and protons, he uses as building units a particles (4 protons + 2 electrons) of mass 4, and hypothetical units of mass 3 with a single positive charge (3 protons + 2 electrons). The matter has been more recently discussed and nucleus models suggested by Rutherford,[16] E. Gehrcke[17] and others.
The fact that the helium nucleus is almost exactly an integer on the oxygen scale that is to say helium has approximately normal packing gives a distinct balance of probability that helium nuclei actually exist as such in the nuclei of normal elements. In support of this idea it has been stated that the presence of helium nuclei inside the nuclei of radioactive atoms is definitely proved by the ejection of a particles by the latter. In the writer's opinion this is much the same as saying that a pistol contains smoke, for it is quite possible that the α particle, like the smoke of the pistol, is only formed at the moment of its ejection. Brosslera[18] defends this view and points out that if the alteration from looser to closer packing of the charges forming the particle is at all large energy will be liberated amply sufficient for the purpose of detaching it and giving it the energy of an α ray. The reason to expect that this energy will be set free will be described in the next section. Brosslera's suggestion that in the nuclei of radioactive atoms there are loosely bound protons and electrons and that these, given something of the nature of a certain exact and instantaneous correlation, might combine to form an a particle is in good accordance with the most reasonable theory of radioactive disintegration, which was first put forward by Lindemann.[19]
There are therefore two different ideas which we may regard as working hypotheses. According to the first the nuclei of atoms consist of helium nuclei, or a particles, held together in some way so that their packing effect upon each other is small; and, in the case of atoms not having a mass of the type 4n, additional protons and electrons. According to the second we only have to suppose that the mean packing of all the charges in the nucleus is such as will account for the whole number rule with sufficient exactness, but that the actual arrangement of the protons and electrons need not necessarily be at all similar to that in a helium nucleus.
The experimental evidence is, so far, definitely in favour of the first of these views. In their remarkable work on the disintegration of light atoms by the collision of swift a rays Rutherford and Chadwick[20] show that as the result of such collisions swift hydrogen rays, i.e. free protons, are liberated from the atoms of boron, nitrogen, fluorine, sodium, aluminium and phosphorus. They point out that the masses of the atoms of all these elements are of the types 4n + 2 and 4n + 3. The effect is not obtained from atoms of the type 4n so that this result suggests that in these the protons are already all bound together to form helium nuclei.
98. Cosmical effects due to change of mass
It has long been known that the chemical atomic weight of hydrogen was greater than one quarter of that of helium, but so long as fractional weights were general there was no particular need to explain this fact, nor could any definite conclusions be drawn from it. The results obtained by means of the mass spectrograph[21] remove all doubt on this point, and no matter whether the explanation is to be ascribed to packing or not, we may consider it absolutely certain that if hydrogen is transformed into helium a certain quantity of mass must be annihilated in the process. The cosmical importance of this conclusion is profound and the possibilities it opens for the future very remarkable, greater in fact than any suggested before by science in the whole history of the human race. We know from Einstein's Theory of Relativity that mass and energy are interchangeable[22] and that in C.G.S. units a mass m at rest may be expressed as a quantity of energy mc2, where c is the velocity of light. Even in the case of the smallest mass this energy is enormous. The loss of mass when a single helium nucleus is formed from free protons and electrons amounts in energy to that acquired by a charge e falling through a potential of nearly thirty million volts. A swift α ray has an energy of three to four million volts so that the change of packing suggested by Brosslera need not be nearly so great to provide the energy needed. If instead of considering single atoms we deal with quantities of matter in ordinary experience the figures for the energy become prodigious.
Take the case of one gramme atom of hydrogen, that is to say the quantity of hydrogen in 9 c.c. of water. If this is entirely transformed into helium the energy liberated will be
- .0077 X 9 X 1020 = 6.93 X 1018 ergs.
Expressed in terms of heat this is 1.66 x 1011 calories or in terms of work 200,000 kilowatt hours. We have here at last a source of energy sufficient to account for the heat of the Sun.[23] In this connection Eddington remarks that if only 10 per cent, of the total hydrogen on the Sun were transformed into helium enough energy would be liberated to maintain its present radiation for a thousand million years.
Should the research worker of the future discover some means of releasing this energy in a form which could be employed, the human race will have at its command powers beyond the dreams of scientific fiction; but the remote possibility must always be considered that the energy once liberated will be completely uncontrollable and by its intense violence detonate all neighbouring substances. In this event the whole of the hydrogen on the earth might be transformed at once and the success of the experiment published at large to the universe as a new star.
99. The stable systems of protons and electrons known to occur.
Starting with our standard bricks, the protons and electrons, we may make, theoretically at least, an infinity of systems by the combination of any number of each. It is interesting to consider the systems actually occurring in practice, that is to say those which are sufficiently stable to give definite evidence of their existence. The following table gives, in order of mass, the first twenty-four known. Where the circles representing the charges touch each other, to form nuclei, the packing is extremely close, where they do not touch they are to be taken as distant thousands of times further from each other. The masses of the first twelve are deduced as follows : The most accurate value for the chemical atomic weight of hydrogen is 1.0077 (O = 16), and as it is very improbable that it consists of isotopes we take this as the mass of a neutral hydrogen atom. The mass of the electron is 0.00054 and as the packing effect is nil we arrive at the figure 1.0072 for the mass of the proton, and this agrees within the experimental error with that directly determined by the mass-spectrograph. The most probable value of the mass of a neutral helium atom is 4.00(0) we will assume the last figure for the sake of simplicity. The masses of (13) to (24) are less accurately known.
The stability, where known, is expressed in volts and represents the potential through which a charge e must fall in order to acquire sufficient energy to disrupt the particular configuration concerned. This is the ionisation potential in the case of atoms.
References
- ↑ The Electron, by R. A. Millikan, University of Chicago Press, 1917.[1]
- ↑ From Greek πρω̃τος first the primary substance.
- ↑ P. 67.
- ↑ V. p. 105.
- ↑ Rutherford, Phil. Mag. 41, 669, 1911.[2]
- ↑ Moseley, Phil. Mag., 26, 1031, 1913.[3]
- ↑ Cf. Barkla, Phil. Mag., 14, 408, 1907.[4]
- ↑ Van den Brock, Phys. Zeit. 14, 33, 1913.[5]
- ↑ Chadwick, Phil. Mag., 140, 734, 1920.
- ↑ Bohr, Phil Mag. 36, 1, 476, 857, 1913.[6]
- ↑ Sommerfeld, Atombau and Spektrallinien, Brunschweig, 1921.[7]
- ↑ Bohr, Nature, 107, 104, 1921.[8]
- ↑ Langmuir, Brit. Assoc. Edinburgh meeting, 1921.
- ↑ J. J. Thomson, Proc. Roy. Soc. 99A, 90, 1921,
- ↑ Harkins, Phys. Rev., 15, 73, 1920.[9]
- ↑ Rutherford, Proc. Roy. Soc, 97A, 374, 1920.[10]
- ↑ Gehrcke, Phys. Zeit, 22, 151, 1921.
- ↑ Brosslera, Rev. Chim., 1, 42, 74, 1921.
- ↑ Lindemann, Phil. Mag., 30, 560, 1915.
- ↑ Rutherford and Chadwick, Phil. Mag., 42, 809, 1921.[11]
- ↑ V. p. 70.
- ↑ Eddington, Time, Space and Gravitation, p. 146, Cambridge, 1920.[12]
- ↑ Eddington, Brit. Assoc, address, 1920; Perrin, Scientia, Nov., 1921.
Francis William Aston (1922), Isotopes, ISBN 978-1016732383, Internet Archive.
