Aston 1922/Chapter 9

Chapter IX - Isotopes and Atomic Numbers

100. The relation between chemical atomic weight and atomic number

Inasmuch as it is now recognised to be in general merely a statistical mean value the importance of the chemical atomic weight has been greatly reduced by the discovery of isotopes. Its position as the natural numerical constant associated with an element has been taken by the atomic number, though from the point of view of chemical analysis the chemical atomic weight is just as important as it ever was.

The possibility of anomalies in the order of the elements in the periodic table when their chemical atomic weights are considered, is now obvious enough. The true weights of the atoms as directly determined, are so intermingled in the order of the natural numbers and the proportions present in complex elements so varied that such anomalies are bound to occur, indeed it is rather surprising there are not more.

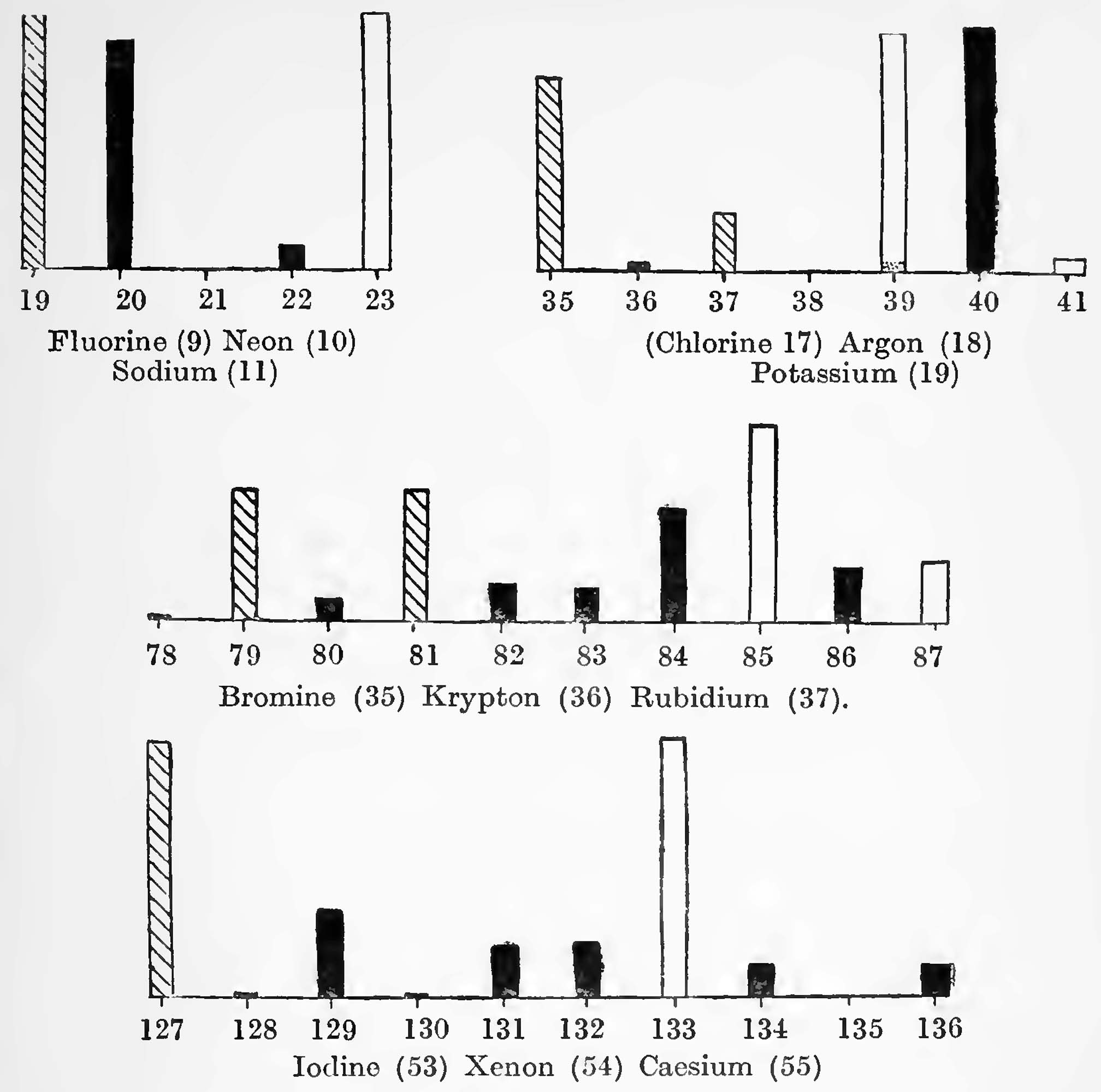
Fig. 17. Isotopes of the Halogens, the inert gases and the alkali metals.

The following table (Fig, 17) shows the masses of the isotopes of three groups of elements now completely investigated. The approximate proportions present are indicated by the heights of the columns; plain for the alliali metals, black for the inert gases, and hatched for the halogens. The anomalous order of argon and potassium is at once seen to be due to the fact that whereas the heavier constituent of argon is present in much the greater proportion, in potassium the reverse is the case. Had the proportions of heavier and lighter isotopes been similar in each case the atomic weight of potassium would have been greater instead of less than that of argon.

101. Statistical relations exhibited by elements and their isotopes

Although our knowledge of true atomic weights is far from complete, for out of eighty-seven existing elements only twenty-seven have been analysed, of which thirteen are simple, interesting relations have already become clear which are stated in the form of rules as follows:

In the nucleus of an atom there is never less than one electron to every two protons.

There is no known exception to this law. It is the expression of the fact that if an element has an atomic number N the atomic weight of its lightest isotope cannot be less than 2N. Worded as above, the exception in the case of hydrogen is avoided. True atomic weights corresponding exactly to 2N are known in the majority of the Ughter elements ip to A³⁶ Among the heavier elements the difference between the weight of the lightest isotope and the value 2N tends to increase with the atomic weight; in the cases of mercury it amounts to 37 units. The corresponding divergence of the mean atomic weights from the value 2N has of course been noticed from the beginning of the idea of atomic number.

The number of isotopes of an element and their range of atomic weight appear to have definite limits. Since the atomic number only depends on the net positive charge in the nucleus there is no arithmetical reason why an element should not have any number of possible isotopes. An examination of the tables of results given on p. 89 and at the end of the book show that so far the largest number determined with certainty is 6 in the case of krypton. It is possible that xenon has even more, but the majority of complex elements have only two each. The maximum difference between the lightest and heaviest isotope of the same element so far determined is 8 units in the cases of krypton and xenon. The greatest proportional difference, calculated on the lighter weight, is recorded in the case of lithium, where it amounts to one-sixth. It is about one-tenth in the case of boron, neon, argon and krypton.

The number of electrons in the nucleus tends to be even. This rule expresses the fact that in the majority of cases even atomic number is associated with even atomic weight and odd with odd. If we consider the three groups of elements, the halogens, the inert gases and the alkah metals, this tendency is very strongly marked. Of the halogens odd atomic numbers all 6 (+1?) atomic weights are odd. Of the inert gases even atomic numbers 13 (+2?) are even and 3 odd. Of the alkali metals odd atomic numbers 7 are odd and 1 even. In the few known cases of elements of the other groups the preponderance, though not so large, is still very marked and nitrogen is the only element yet discovered to consist entirely of atoms whose nuclei contain an odd number of electrons.

A further interesting result is the absence of isobares. So far none have been definitely identified, but it is quite obvious that in the cases of elements such as calcium and selenium they must exist, for the supply of integers in the region of their atomic weights have been exhausted by the needs of other elements.

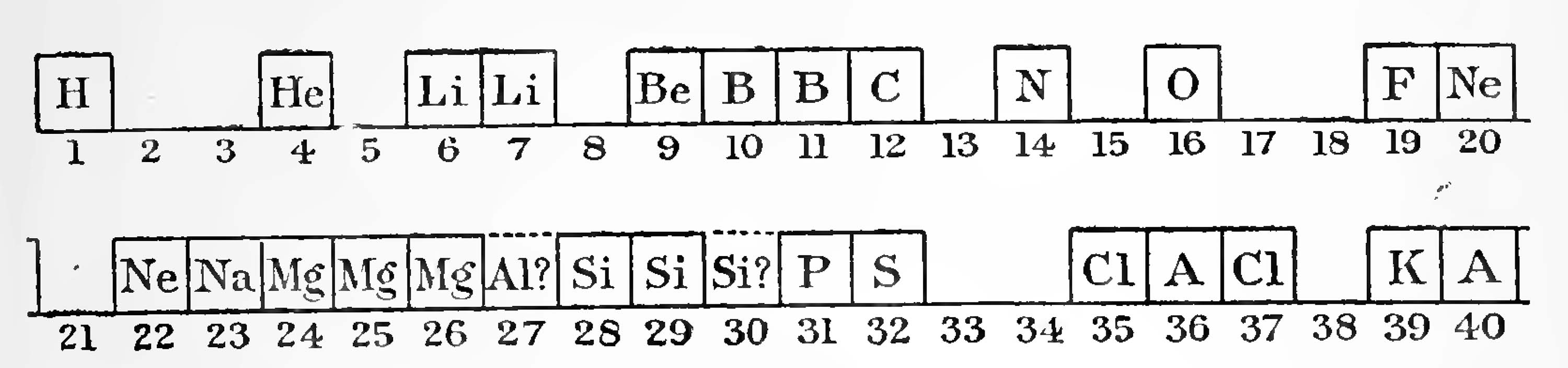
Fig. 18. The first 40 natural numbers, showing those occupied by atomic weights of known elements.

A table of the first 40 natural numbers and the true atomic weights corresponding to them is given in Fig. 18. The gaps are particularly interesting and seem to show no semblance of regularity. It is very clear that many more experimental results will have to be obtained before any satisfactory theory for the occurrence of these, or of the other laws, is to be formulated.

102. The preponderance of elements of even atomic number

In discussing the nuclear structure of elements the question of their relative abundance in nature is one of great interest. This may be estimated by direct chemical analysis of the Earth's crust, and such extra-terrestrial sources as are available in the form of meteorites. The spectroscope will tell us what elements are present in the stars, but unfortunately it does not give much direct information as to their relative quantities.

On this question we can classify to use biological terms either by individuals or by species. We may examine the percentage composition, which wiU give a measure of the total number of individual atoms of each element present, or we may inquire into the number of different nuclear species which occur and classify them without respect to their individual abundance.

A very valuable discussion from the first point of view has been published by Harkins,^[1] who considers the percentage composition of meteorites and of parts of the Earth's crust. He demonstrates in a most convincing manner that there are immensely more atoms of elements of even atomic number. This interesting preponderance can, with a reasonable amount of probability, now be extended to even atomic weight, by the statistics given in the preceding paragraphs, but it will not be certain until the constitution of certain abundant elements such as iron has been actually determined.

The second point of view can be examined by means of the atomic weights of the radioactive isotopes and also by the true atomic weights given by the mass-spectra. In both cases nuclear systems of even atomic number are found to predominate. The mass-spectra of 13 elements of even, and 14 elements of odd atomic number indicate 32 isotopes of even atomic number and 20 of odd. The average element of even atomic number has therefore 2-5 isotopes to 1-4 for each element of odd atomic number.

The table on p. 15 shows that among the radioactive isotopes the preponderance is greater 32 as against 10 but it is possible that the former figure may include some atomic systems absolutely identical though of different origin.

103. The constancy of chemical atomic weights

One of the first difficulties in the way of accepting the idea of the complex constitution of an element such as chlorine was the constancy of its atomic weight. This had been determined by many different observers using different methods and the results were always the same within a very small experimental error. This difficulty may be met, in the first place, by noting that the vast majority, if not all, of the really accurate values were obtained from chlorine which must have been originally derived from the sea. The sea has been mixed for so long that it would be absurd to expect to find chlorines of different chemical atomic weights in it. Had ordinary galena been the only source of lead used in the atomic weight determinations given on page 16 no difference would have been found. It was only by examining the lead from extraordinary radioactive sources that the results were obtained which gave such definite and valuable support to the theory of isotopes.

The atomic weight of chlorine from sources other than the sea is now receiving the attention of chemists, though it is naturally very difficult to be at all sure that any known source of chlorine is not of marine origin. Mile. Irene Curie^[2] has examined the atomic weight of chlorine from three minerals whose marine origin seems unlikely. The values obtained from a sample of sodalite (sodium aluminium chlorosilicate) from Canada, and from a sample of calcium chlorophosphate from Norway agree with the value for chlorine from sea-water. The value 35.60, for chlorine from a sample of sodium chloride from a desert region in Central Africa was slightly high.

The comparison of the atomic weights of terrestrial and meteoric nickel made by Baxter and Parsons^[3] is interesting in this connection. As a mean of nine determinations with the terrestrial material the figure 58.70 was found, whilst three experiments with meteoric nickel gave 58.68. The standard value found by Richards and Cushman was 58.68 (Ag = 107.88). The difference found between terrestrial and meteoric nickel is considered to be within the limits of experimental error, but further comparisons are to be made.

The writer regards these negative results as having a cause probably much more fundamental than the mere mechanical mixing of the different constituent isotopes during the history of the body containing them, namely a constancy of proportion during the evolution of the elements themselves. This will be considered later. The case of the radioactive leads is entirely exceptional. These substances have been produced continuously during the history of the earth's crust and are being so produced to-day. Although ordinary lead may consist of isotopes which is practically certain and these isotopes may be identical in every respect with those produced in the last stage of radioactive disintegration, yet there is no reason whatever to assume that ordinary lead is itself the accumulated result of these processes. It takes its place among the other ordinary elements and would doubtless have done so had thorium and uranium never existed.

104. The agreement between the chemical atomic weight and the mean atomic weight deduced from the mass spectrum

The mean atomic weight of the isotopes of a complex element can be calculated if the relative intensities of their lines in the mass-spectrum is known. This has been directly measured by Dempster.^[4] The charged particles of isotopes of the same element are practically certain to affect the photographic plate to the same extent as each other, hence we can obtain a rough estimate of their relative proportion by comparing the intensities of the lines. If this is done it is found that the great majority of the elements so far tested give mean results in good agreement with the accepted chemical values. The following table gives the data concerning four in which the difference is noteworthy:

The case of boron is the most difficult to account for. The masses of its isotopes 10 and 11 certainly do not differ from integers by more than one or two parts in a thousand. The ratio of the intensities of their second order lines 5 and 5.5 (and there were no other substances present which could possibly give such lines) is equally certainly not as high as 9:1. It was for this reason that a third isotope 12 was suspected, but as no evidence of this has been found it seems most probable that the chemical atomic weight is still slightly too high.

The atomic weights of krypton and xenon are not of course chemical in the ordinary sense, as they are deduced direct from density determinations. Any trace of the impurity most likely to be present, argon in the first case, krypton in the second, would tend to make the densities too low, and this appears the most likely explanation.

In the case of caesium the chemical result may be correct, for the probable error in the determination of mass is at least as large as the discrepancy. On the other hand caesium appears to be a simple element, in which case its chemical atomic weight must represent the true weight of its atoms. Any error in this figure would probably be of the sign suggested, for it is the heaviest member of its chemical group. If, however, as is possible, the true mass of its atom differs from an integer by as much as 0.2 it is a fact of the greatest interest.

105. The meaning of the word "element."

The exact idea conveyed by the word "element"in chemistry and physics has given rise to endless difficulties in the past. In this connection Crookes in 1886 sums up the matter as follows :

"Of the attempts hitherto made to define or explain an element, none satisfy the demands of the human intellect. The textbooks tell us that an element is 'a body which has not been decomposed'; that it is 'a something to which we can add, but from which we can take away nothing,' or 'a body which increases in weight with every chemical change.' Such definitions are doubly unsatisfactory: they are provisional, and may cease to-morrow to be applicable to any given case. They take their stand, not on any attribute of things to be defined, but on the limitations of human power; they are confessions of intellectual impotence."

There was good reason for this dissatisfaction. The discovery ten years later of the electron, and the subsequent electrical theory of matter robbed the word of any pretence to its original meaning; for although Ramsay attempted to introduce into chemistry electricity itself as an element, it soon became obvious that this extension was unsuitable. The discovery of isotopes brings us face to face with two possible alternatives. The first is to call each isotope, as it is discovered, a new element. The second is to fix the word precisely, now and for the future, as meaning a substance with definite chemical and spectroscopic properties which may or may not be a mixture of isotopes in other words to associate it exclusively with the conception of atomic number. On this view there would be, corresponding to Moseley's numbers, 92 possible elements, of which 87 are known.

If we adopt the first of these alternatives a new word will be necessary to express such substances as chlorine or magnesium, hitherto called elements, and also the word element would mean something entirely different from what it has meant in all the chemical and physical literature of the past century. It would moreover be still subject to alterations in the future.

In the opinion of the writer the second alternative the association of element with atomic number is much the more preferable. The difficulties arising from it are practically confined to the radioactive substances which can differ from one another even when their atomic numbers and atomic weights are identical. This is not very serious, for the radioactive elements are in a class by themselves and the special nomenclature already applied to them could be retained or revised as convenient without affecting that of general chemistry.

106. Disintegration theory of the evolution of the elements

A theory has been put forward by some writers that all the elements occurring in nature are the result of radioactive disintegrations of the ordinary type, but continued far beyond the ordinary limit observed at present. For instance, if we continue the a ray changes of the thorium series far enough we shall ultimately reach helium. The emission of an α particle is the only change known to occur which alters the atomic weight and it always does so by 4 units at a time. Hence from thorium we shall get a series of elements or isotopes of atomic weights from 232 to 4 of the general type 4n. Uranium in the same way will yield a similar series of the type 4n + 2. In order to obtain isotopes of odd atomic weight it is necessary to postulate parent elements of the type 4n + 1 and 4n + 3.

Using hypotheses based on this general idea Van den Broek,^[5]Harkins,^[6] Kohlweiler,^[7] Kirchoff^[8] and others have built up the most elaborate systems of isotopes,

The writer regards this view as unlikely and misleading. In the first place it does not appear to succeed in its objects. As an explanation of how the elements may have been evolved it starts with at least four elements as complicated as any known to exist, which does not advance the inquiry very much. On the other hand it may be used to predict the atomic weights of the isotopes composing known elements, and a great many predictions of this kind have been made. Here, though the measure of its success has varied to some extent with the particular modification of the theory employed, it has never been worthy of serious consideration. In cases where two or three isotopes of a given element were predicted they proved as often wrong as right, and when the number of isotopes of integral atomic weights was so large that some agreements were inevitable the argument obviously loses all its force.

Another objection is that radioactive transformations do not continue, as far as we can see, beyond the stage (lead) indicated in the diagrams on p. 15. The lighter elements are definitely not radioactive. The radioactivity of potassium and rubidium is exceedingly small and its nature doubtful; in any case it is best ascribed to minute vestiges of radioactive isotopes, not to feeble radioactivity of the main constituents. It seems therefore more reasonable, for the present, to regard the property of radioactivity as absent entirely from the inactive elements than to suppose it present but too weak to be detected. It must not be gathered from these remarks that it is considered impossible to imagine physical conditions violent enough to disrupt the nuclei of light atoms, but rather that the mechanism causing such disruption need not be similar in any way to that causing normal radioactivity.

107. Crookes' theory of the evolution of the elements

A more attractive theory than the one given above is that the complex atoms of matter have been evolved by the aggregation of simpler atoms. This idea has received a good deal of attention in the past. Crookes^[9] remarks on it as follows:

"Let us picture the very beginnings of time, before geological ages, before the earth was thrown off from the central nucleus of molten fluid, before even the sun himself had consolidated from the original pivtyle. Let us still imagine that at this primal stage all was in an ultra-gaseous state, at a temperature inconceivably hotter than anything now existing in the visible universe; so high indeed that the chemical atoms could not yet have been formed, being still far above their dissociation point. In so far as protyle is capable of radiating or reflecting light, this vast sea of incandescent mist, to an astronomer in a distant star, might have appeared as a nebula, showing in the spectroscope a few isolated hues, forecasts of hydrogen, carbon and nitrogen spectra.

"But in due course of time some process akin to cooling, probably internal, reduces the temperature of the cosmic protyle to a poimt at which the first step in granulation takes place; matter as we know it comes into existence, and atoms are formed."

This vivid picture may be brought up to date by the substitution of free protons and electrons for the hypothetical protyle. We can imagine regions containing matter where the temperature is so high that not only is the dissociation of atoms from atoms and nuclei from planetary electrons complete but also protons and electrons are in a state of agitation so violent that even the most stable nuclei cannot be formed. We should have here matter of the simplest form we can imagine, or rather of no form at all, simply a more or less neutral electric gas. Such a condition is by no means impossible in our universe and may actually occur during one of those excessively violent catastrophes occurring in far distant space and observed by us as new stars.

By some such cooling process as that suggested by Crookes we easily imagine the free charges combining to form the nuclei of elements. Whether those of heavier elements are formed direct by the charges getting into particular geometrical relations with each other, or whether helium nuclei are formed first and then subsequently coalesce depends on which theory of nuclear structure is adopted. In any case vast quantities of energy will have to be radiated off and this radiation may be of such extremely high frequency that it is capable of disrupting nuclei themselves, so that there might be at this stage rapid and continuous transformations from heavier to lighter nuclei and vice versa.

For the present we are interested in the number of each type of atom which survives. It is obvious that if the conditions of cooling are practically identical throughout the whole mass there is no reason why the composition of the matter produced should vary. If 3 atoms of Cl³⁵ are formed to every 1 of Cl³⁷ at any one point the same ratio must hold at every point so that a complex element of constant atomic weight will be formed. But it is much more likely that different parts of this primordial mass will undergo their transformations under different rates of cooling, etc., so it is worth while inquiring if variation in the mean atomic weight of a complex element is to be expected.

The quantity of one particular atomic nucleus formed will probably depend (a) on the probability of a certain configuration of charges happening as a chance event; (b) the stability of the particular nucleus formed as the result of that event. Again to take the case of chlorine each isotope may be regarded as completely stable and the relative quantities formed will simply depend on condition (a). Now it is not unreasonable to suppose that this is not seriously affected by different rates of cooling, and in this case the isotopes will be evolved in constant proportion. As we know of no natural process by which the proportion of isotopes can be altered appreciably the complex elements will have to-day the same chemical atomic weight as when they were first formed.

The above argument is of course purely a speculative one, and the conclusion drawn from it would fall to the ground at once if noteworthy differences of atomic weight in a single complex element were found supposing that element was not the product of a radioactive change at different points on the earth's surface. It may be worth noting that condition (a) suggests that, in general, the lighter atoms will outnumber the heavier ones. In all matter available in nature this preponderance is actually enormous.

If the matter forming the earth ever went through a primordial stage such as that suggested above it certainly did so more than 10⁹ years ago. It follows that of the radioactive elements then formed only two, thorium and uranium, will now be found on the earth, for the other radioactive elements existing to-day are of such short period that they must have been formed since. Hence we may divide the original elements very simply and definitely into two groups: (1) All the inactive elements, whose nuclei are sufficiently simple to be stable; (2) Thorium and Uranium, whose nuclei are so complex that they are only partially stable.

Other less stable elements may have been formed then but there can be no proof of this for they would, in any case, have disappeared long ago, and it is clear that the other radioactive elements now found can all be regarded as formed from the two parent elements in comparatively recent times.

References

↑ Harkins, Jour. Amer. Chem. Soc, 39, 856, 1917.[1]
↑ I Curie, Compt. Retid. 172, 1025, 1921.[2]
↑ Baxter and Parsons, Jour. Amer. Chem. Soc, 43, 607, 1921.[3]
↑ V. p. 81.
↑ Van den Broek, Phys. Zeit., 17, 260, 579, 1916; 23, 164, 1921.
↑ Harkins and Wilson, Jour. Am. Chem. Soc, 37, 1367, 1915; Harkins and Hall, ibid., 38, 169, 1916; Harkins, Phys. Rev., 15, 73, 1920; Nature, 105, 230, 1920; Jour. Amer. Chem. Soc, 42, 1956, 1920; Phil. Mag., 42, 305, 1921.
↑ Kohlweiler, Zeit. fur Physikal. Chem., 94, 513, 1920; Phys. Zeit., 21, 311, 543; 22, 243, 1921.
↑ Kirchoff, ibid., 21, 711, 1920.
↑ Crookes, Brit. Assoc, address, 1886.